Ionizing Radiation

What is Ionizing Radiation?

Ionizing radiation is energy in the form of waves or particles that has enough force to

remove electrons from atoms (USEPA).

Radiation that falls within the ionizing radiation" range has enough energy to remove tightly bound electrons from atoms, thus creating ions. This is the type of radiation that people usually think of as 'radiation.' We take advantage of its properties to generate electric power, to kill cancer cells, and in many manufacturing processes.

and..

Radiation that has enough energy to move atoms in a molecule around or cause them to vibrate, but not enough to remove electrons, is referred to as "non-ionizing radiation." Examples of this kind of radiation are sound waves, visible light, and microwaves.

The energy of the radiation shown on the spectrum below increases from left to right as the frequency rises.

Longer wave length, lower frequency waves (heat and radio) have less energy than shorter wave length, higher frequency waves (X and gamma rays). Not all electromagnetic (EM) radiation is ionizing. Only the high frequency portion of the electromagnetic spectrum which includes X rays and gamma rays is ionizing (WHO).

What is Radon

About Radon, (source: WHO)

Radon is a chemically inert, naturally occurring radioactive gas. It has no smell, colour or taste. Radon is produced from the natural radioactive decay of uranium, which is found in rocks and soil. Radon can also be found in water.

Radon escapes easily from the ground into the air, where it

disintegrates through short-lived decay products called radon progeny. As radon progeny decay, they emit radioactive alpha particles and attach to aerosols, dust and other particles in the air. As we breathe, radon progeny are deposited on the cells lining the airways where the alpha particles can damage DNA and potentially cause lung cancer.

Outdoor radon levels are usually very low. The average outdoor radon level varies between 5 and 15 Bq/m3 [Radon radioactivity is measured in Becquerel (Bq). One Becquerel corresponds to the transformation (disintegration) of one atomic nucleus per second. Radon concentration in air is measured by the number of transformations per second in a cubic metre of air (Bq/m3)]. Indoors, radon levels are higher, with highest levels found in places such as mines, caves and water treatment facilities.

Exposure of radiation:

(Source: WHO)

How Radon enters a house?

Radon enters homes through:

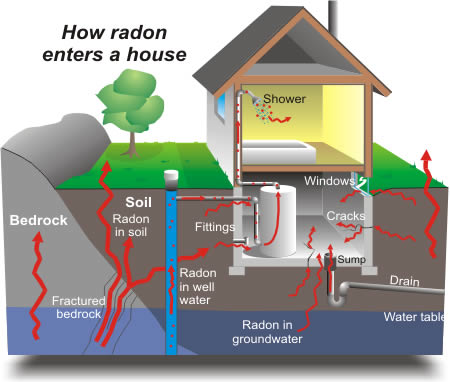
• cracks at concrete floor-wall junctions
• gaps in the floor
• small pores in hollow-block walls
• sumps and drains.

(source: www.prlog.org)

Radon levels in homes can be reduced by:

• improving the ventilation of the house
• avoiding the passage of radon from the basement into living rooms
• increasing under-floor ventilation
• installing a radon sump system in the basement
• sealing floors and walls
• installing a positive pressurization or ventilation system.

(source: http://www.ab.ust.hk/hseo/sftywise/199504/page1.htm)

Risk Assessment (source)

Exposure to radon, no matter how much exposure, does not mean you will get lung cancer. The risks associated with contracting lung cancer are in relationship to the amount of time exposed and the average Radon concentration levels.

Most radiation protection specialists believe, (at a minimum), that if you are continuously exposed to levels at or above 4 pCi/L then you are at risk. The US EPA's action level for Radon is 4 pCi/L. The World Health Organization has recently suggested that the action level should be 2.7 pCi/L, 33% lower than the current EPA action level.

The EPA has identified radon exposure as the number one cause of lung cancer in non smokers, and second only to smoking overall. Smokers generally have about 10 times higher risk than non smokers. Risk assessments associated with elevated radon concentrations are considered to be linear, meaning higher levels and longer duration of exposure increase risk assessment accordingly to the increase in concentration and amount of time exposed.

EPA risk assessment data from radon exposure is based on a lifetime of exposure.

• Not everyone exposed to even high levels of radon will contract radon induced lung cancer.
• All radon levels can be lowered, which lowers the risk assessment.

read more about radon:

UNCEAR: Sources to effects assessment for radon in homes and workplaces

WHO: WHO HANDBOOK ON INDOOR RADON: A PUBLIC HEALTH PERSPECTIVE

Gamma Spectrometry - Efficiency Calculation for K-40

Gamma Efficiency for K-40

Activity

Define activity, A = Number of spontaneous disintegrations in a source in one second.

Unit of activity, A = Bq (Becquerel)

Activity, A

N = Number of atom for K40

λ = Decay constant

t = Time

Specific Activity

Half-life

λ is a decay constant, therefore

How to calculate Activity and efficiency of K40 in KCl for Gamma Spectrometry

(eg. Standard KCl, 400g was used to calibrate the gamma spectrometry)

a) Calculate Mass of K in KCl

=

b) Calculate Mass K40 in 209.779 g K

=
=
= g

c) Calculate Number of atom K40

d) Calculate Decay constant, λ for K40

e) Calculate Activity K40 in KCl

f) Efficiency K40 for Gamma Spectrometry

(eg. Counting time = 43200 s, peak area = 140 000)

Statistic - Q test

Theory

In a set of replicate measurements of a physical or chemical quantity, one or more of the obtained values may differ considerably from the majority of the rest. In this case there is always a strong motivation to eliminate those deviant values and not to include them in any subsequent calculation (e.g. of the mean value and/or of the standard deviation). This is permitted only if the suspect values can be "legitimately" characterized as outliers.

Usually, an outlier is defined as an observation that is generated from a different model or a different distribution than was the main "body" of data. Although this definition implies that an outlier may be found anywhere within the range of observations, it is natural to suspect and examine as possible outliers only the extreme values.

The rejection of suspect observations must be based exclusively on an objective criterion and not on subjective or intuitive grounds. This can be achieved by using statistically sound tests for "the detection of outliers".

The Dixon's Q-test is the simpler test of this type and it is usually the only one described in textbooks of Analytical Chemistry in the chapters of data treatment. This test allows us to examine if one (and only one) observation from a small set of replicate observations (typically 3 to 10) can be "legitimately" rejected or not.

Q-test is based on the statistical distribution of "subrange ratios" of ordered data samples, drawn from the same normal population. Hence, a normal (Gaussian) distribution of data is assumed whenever this test is applied. In case of the detection and rejection of an outier, Q-test cannot be reapplied on the set of the remaining observations.

In statistics, Dixon's Q test, or simply the Q test, is used for identification and rejection of outliers. This test should be used sparingly and never more than once in a data set. To apply aQ test for bad data, arrange the data in order of increasing values and calculate Q as defined:

Where gap is the absolute difference between the outlier in question and the closest number to it. If Q_calculated > Q_table then reject the questionable point.

EXAMPLE:

For the data:

0.189, 0.167, 0.187, 0.183, 0.186, 0.182, 0.181, 0.184, 0.181, 0.177

Arranged in increasing order:

0.167, 0.177, 0.181, 0.181, 0.182, 0.183, 0.184, 0.186, 0.187, 0.189

Outlier is 0.167. Calculate Q:

With 10 observations, Q_calculated (0.455) > Q_table (0.412), so reject it with 90% confidence. However, at 95% confidence, Q_calculated (0.455) < Q_table (0.466).

Therefore keep 0.167 at 95% confidence or reject it at 90% confidence.

TABLE

This table summarize the limit values of the test.

(sources: wikipedia, http://www.chem.uoa.gr/applets/AppletQtest/Text_Qtest2.htm)